QC検定3級|正規分布と二項分布、確率の求め方を例題で解説
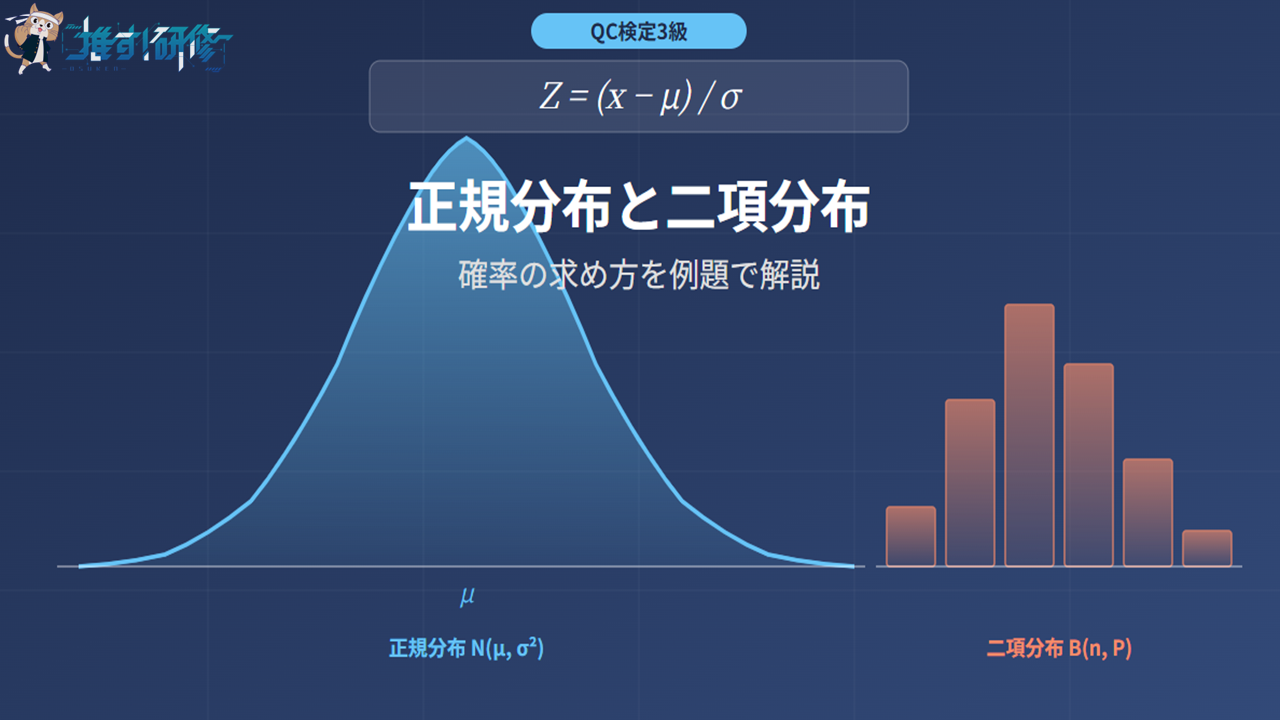
QC検定3級の「統計的方法の基礎」で、多くの受験者がつまずくのが正規分布と二項分布です。正規分布表の読み方がわからない、標準化の計算で手が止まる、二項分布との違いがあいまい——こうした悩みを抱えていませんか?
この記事では、正規分布と二項分布の基本的な考え方から、標準化の計算手順、正規分布表の具体的な使い方、そして試験で頻出の確率の求め方パターンまでを、例題を交えてわかりやすく解説します。
QC検定3級では、正規分布の出題頻度が非常に高く、ここを確実に得点できるかどうかが合否を分けるポイントになります。数学や統計に苦手意識がある方でも理解できるように、計算の一つひとつを丁寧に追っていきますので、安心して読み進めてください。
正規分布とは?|計量値の分布を理解しよう
品質管理の現場では、「不良品がどれくらいの割合で出るのか」をあらかじめ予測できると、対策が立てやすくなります。そのために必要なのが「確率と分布」の考え方です。
確率とは、ある出来事がどれくらい起こりやすいかを表す数字です。たとえば、サイコロを振って1が出る確率は6分の1(約16.7%)です。これと同じように、工場で作った製品の重さや長さについても、「ある値になる確率はどれくらいか」を考えることができます。
たとえば、同じ工場で同じペットボトル飲料を作っても、内容量はぴったり500mlにはなりません。499mlのときもあれば、501mlのときもあります。このように、データには必ずばらつきがあります。
しかし、このばらつき方はデタラメではありません。実は一定のルールに従っていて、「どのような値が、どれくらいの確率で現れるか」はあらかじめ決まっています。このばらつき方のルールのことを分布(確率分布)といいます。
QC検定3級で出題される分布は、正規分布と二項分布の2つです。正規分布は計量値(長さや重さなど、連続した値)の分布を表し、二項分布は計数値(不適合品数や人数など、1つ、2つと数えられる値)の分布を表します。
正規分布の形と特徴
正規分布の形には、次のような特徴があります。
- 左右対称の釣鐘型(お寺の鐘を横から見たような形)
- 山の頂上は必ず1つだけ
- 左右が非対称になったり、山が2つになることはない
イメージとしては、クラス全員のテストの点数をグラフにしたときの形を思い浮かべてください。平均点のあたりに一番多くの人が集まり、そこから離れるほど人数が少なくなっていく、あの山型のグラフが正規分布です。
山の高さや裾の広がり方は、データによって変わります。ばらつきが小さいデータなら細長い山になり、ばらつきが大きいデータなら横に広がった山になります。
正規分布のパラメータ:平均μと分散σ²
では、正規分布の山の形は何によって決まるのでしょうか。それが、平均μ(ミュー)と分散σ²(シグマの二乗)という2つのパラメータです。パラメータとは、分布の形を決める要素のことです。
正規分布はN(μ, σ²)と表します。試験の問題文では、「○○のデータは正規分布N(μ, σ²)に従う」という書かれ方をします。
平均μは「山の中心がどこにあるか」を表し、分散σ²は「山がどれくらい横に広がっているか」を表します。平均μが山の位置を決め、分散σ²が山の形を決める——このイメージを持っておくと理解しやすくなります。
ここでいう平均μと分散σ²は、母集団(調べたい対象の全体)の平均と分散のことで、正確にはそれぞれ母平均、母分散といいます。母分散σ²は母標準偏差σの二乗なので、正規分布のパラメータは「母平均と母標準偏差」と書かれることもあります。
なお、平均値x̄、不偏分散V、標準偏差sは、母集団の一部を取り出して計算した値です。母集団全体のパラメータとは意味が異なるため、記号も違うものを使います。この違いは試験でもよく問われるポイントです。
標準正規分布 N(0, 1²) とは
正規分布の中でも特別なものがあります。平均μが0、分散σ²が1の正規分布N(0, 1²)を、標準正規分布といいます。
なぜ特別かというと、正規分布表はこの標準正規分布N(0, 1²)をもとに作られているからです。つまり、どんな正規分布でも、標準正規分布に変換しさえすれば、正規分布表を使って確率を求めることができるのです。
この変換作業のことを「標準化(規準化)」といいます。次のセクションで、標準化の具体的な計算方法を見ていきましょう。
標準化(Z変換)の計算方法
正規分布N(μ, σ²)を標準正規分布N(0, 1²)に変換する作業が「標準化」です。やっていることは、「今あるデータを、平均0・分散1の世界に置き換える」ことです。標準化を行えば、どんな正規分布でも、1つの共通の表(正規分布表)を使って確率が求められるようになります。
標準化の式:Z =(x − μ)/ σ
標準化の式は次の通りです。
Z = (x − μ) / σ
それぞれの意味を確認しましょう。
- x:確率を求めたい値(たとえば「○g以下になる確率」の○にあたる数字)
- μ:平均(正規分布の中心の値)
- σ:標準偏差(ばらつきの大きさ)
- Z:標準化された値(これを使って正規分布表を読む)
この式が意味しているのは、「xが平均μからどれだけ離れているかを、標準偏差σの何個分かで表す」ということです。
この式は必ず覚えてください。試験では、問題文で与えられたμ、σ、xの値をこの式にあてはめて計算するだけで解ける問題が多く出題されます。
標準化の計算例
具体例で確認しましょう。
ある工場で生産しているボルトの長さは、平均μ = 50mm、標準偏差σ = 2mmの正規分布に従っています。このとき、「長さが46mm以下になる確率」を求めるために標準化を行います。
Z = (x − μ) / σ = (46 − 50) / 2 = −2.0
計算結果のZ = −2.0は、「46mmという値は、平均50mmから標準偏差2mmの2個分だけ下(左)にある」ということを意味しています。
Zは標準正規分布N(0, 1²)に従います。このZの値を使って、次のステップで正規分布表から確率を読み取ります。
正規分布表の使い方|KPからPを求める
正規分布に従うデータから確率を求める問題は、QC検定3級で非常によく出題されます。ここでは、正規分布表の読み方と、確率を求めるための3つのパターンを解説します。
まず、この記事で使用する正規分布表を掲載します。試験では問題用紙の最後に正規分布表が載っているので覚える必要はありませんが、読み方を練習するために活用してください。
正規分布表(I)KPからPを求める表
標準化で求めたZの絶対値をKPとして、対応する確率Pを読み取る表です。
| KP | *=0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0* | .5000 | .4960 | .4920 | .4880 | .4840 | .4801 | .4761 | .4721 | .4681 | .4641 |
| 0.1* | .4602 | .4562 | .4522 | .4483 | .4443 | .4404 | .4364 | .4325 | .4286 | .4247 |
| 0.2* | .4207 | .4168 | .4129 | .4090 | .4052 | .4013 | .3974 | .3936 | .3897 | .3859 |
| 0.3* | .3821 | .3783 | .3745 | .3707 | .3669 | .3632 | .3594 | .3557 | .3520 | .3483 |
| 0.4* | .3446 | .3409 | .3372 | .3336 | .3300 | .3264 | .3228 | .3192 | .3156 | .3121 |
| 0.5* | .3085 | .3050 | .3015 | .2981 | .2946 | .2912 | .2877 | .2843 | .2810 | .2776 |
| 0.6* | .2743 | .2709 | .2676 | .2643 | .2611 | .2578 | .2546 | .2514 | .2483 | .2451 |
| 0.7* | .2420 | .2389 | .2358 | .2327 | .2296 | .2266 | .2236 | .2206 | .2177 | .2148 |
| 0.8* | .2119 | .2090 | .2061 | .2033 | .2005 | .1977 | .1949 | .1922 | .1894 | .1867 |
| 0.9* | .1841 | .1814 | .1788 | .1762 | .1736 | .1711 | .1685 | .1660 | .1635 | .1611 |
| 1.0* | .1587 | .1562 | .1539 | .1515 | .1492 | .1469 | .1446 | .1423 | .1401 | .1379 |
| 1.1* | .1357 | .1335 | .1314 | .1292 | .1271 | .1251 | .1230 | .1210 | .1190 | .1170 |
| 1.2* | .1151 | .1131 | .1112 | .1093 | .1075 | .1056 | .1038 | .1020 | .1003 | .0985 |
| 1.3* | .0968 | .0951 | .0934 | .0918 | .0901 | .0885 | .0869 | .0853 | .0838 | .0823 |
| 1.4* | .0808 | .0793 | .0778 | .0764 | .0749 | .0735 | .0721 | .0708 | .0694 | .0681 |
| 1.5* | .0668 | .0655 | .0643 | .0630 | .0618 | .0606 | .0594 | .0582 | .0571 | .0559 |
| 1.6* | .0548 | .0537 | .0526 | .0516 | .0505 | .0495 | .0485 | .0475 | .0465 | .0455 |
| 1.7* | .0446 | .0436 | .0427 | .0418 | .0409 | .0401 | .0392 | .0384 | .0375 | .0367 |
| 1.8* | .0359 | .0351 | .0344 | .0336 | .0329 | .0322 | .0314 | .0307 | .0301 | .0294 |
| 1.9* | .0287 | .0281 | .0274 | .0268 | .0262 | .0256 | .0250 | .0244 | .0239 | .0233 |
| 2.0* | .0228 | .0222 | .0217 | .0212 | .0207 | .0202 | .0197 | .0192 | .0188 | .0183 |
| 2.1* | .0179 | .0174 | .0170 | .0166 | .0162 | .0158 | .0154 | .0150 | .0146 | .0143 |
| 2.2* | .0139 | .0136 | .0132 | .0129 | .0125 | .0122 | .0119 | .0116 | .0113 | .0110 |
| 2.3* | .0107 | .0104 | .0102 | .0099 | .0096 | .0094 | .0091 | .0089 | .0087 | .0084 |
| 2.4* | .0082 | .0080 | .0078 | .0075 | .0073 | .0071 | .0069 | .0068 | .0066 | .0064 |
| 2.5* | .0062 | .0060 | .0059 | .0057 | .0055 | .0054 | .0052 | .0051 | .0049 | .0048 |
| 2.6* | .0047 | .0045 | .0044 | .0043 | .0041 | .0040 | .0039 | .0038 | .0037 | .0036 |
| 2.7* | .0035 | .0034 | .0033 | .0032 | .0031 | .0030 | .0029 | .0028 | .0027 | .0026 |
| 2.8* | .0026 | .0025 | .0024 | .0023 | .0023 | .0022 | .0021 | .0021 | .0020 | .0019 |
| 2.9* | .0019 | .0018 | .0018 | .0017 | .0016 | .0016 | .0015 | .0015 | .0014 | .0014 |
| 3.0* | .0013 | .0013 | .0013 | .0012 | .0012 | .0011 | .0011 | .0011 | .0010 | .0010 |
| 3.5 | .2326E-3 | |||||||||
| 4.0 | .3167E-4 | |||||||||
| 4.5 | .3398E-5 | |||||||||
| 5.0 | .2867E-6 | |||||||||
| 5.5 | .1899E-7 | |||||||||
※表の見方:KP = 2.00のPを求めるには、「2.0*」の行と「*=0」の列が交わるところを読みます。P = .0228(2.28%)です。
正規分布表の読み方
正規分布表には、大きく分けて2種類の表があります。
- (I) KPからPを求める表:「KPがこの値のとき、確率Pはいくつか?」を調べる表
- (II)(III) PからKPを求める表:「確率Pがこの値のとき、KPはいくつか?」を調べる表
上の表(I)を使って、具体的な読み方を確認しましょう。
標準化で求めたZの絶対値をKPとします。「KPの行」と「小数第2位の列」が交わるところの数値を読み取る——これだけです。
先ほどのボルトの例で確認してみましょう。Z = −2.0でしたので、|Z| = KP = 2.00です。表(I)で「2.0*」の行と「*=0」の列が交わるところを見ると、0.0228と読み取れます。つまり、ボルトの長さが46mm以下になる確率は約2.28%です。
100本作ったら約2本が46mm以下になる計算です。こう考えると、確率が身近に感じられるのではないでしょうか。
ここで1つ、大切な用語を確認しておきます。絶対値とは、プラスかマイナスかを無視して、数字の大きさだけを見た値のことです。記号では|Z|と書きます。たとえば、Z = −3のとき|Z| = 3、Z = 3のとき|Z| = 3です。マイナスの符号を外すだけなので、難しく考える必要はありません。
確率の求め方:3つのパターン
正規分布の確率を求める問題は、次の3つのパターンに分類できます。どのパターンかを見極めるコツは、必ず図を描くことです。図を描けば、求めたい確率がどの部分の面積にあたるのかが一目でわかります。
パターン①:○以下(または△以上)の確率をそのまま読み取れるケース
正規分布は左右対称の形をしています。そのため、「平均よりも左側の裾の面積」と「平均よりも右側の裾の面積」は、平均からの距離が同じであれば同じ値になります。このパターンでは、正規分布表から読み取った確率をそのまま答えにできます。これが最もシンプルなパターンです。
パターン②:「1 − 片側の裾」で求めるケース
たとえば、「ある値以上の確率」を求めたいけれど、その値が平均に近い位置にあるため、裾の面積だけでは足りないケースです。正規分布全体の面積は1(= 100%)なので、「全体(1)から反対側の裾の面積を引く」ことで確率を求めます。
パターン③:「1 − 両端の裾」で求めるケース
「○以上△以下の確率」のように、真ん中の部分の面積を求めたいケースです。この場合は、「全体(1)から左側の裾の面積と右側の裾の面積をそれぞれ引く」ことで確率を求めます。
慣れないうちは、毎回かならず釣鐘型の山を描いて、「自分が求めたい面積はどこか?」を塗りつぶしてから計算に入りましょう。この習慣をつけるだけで、ミスが大幅に減ります。
PからKPを求める表の使い方
ここまでは「KPの値から確率Pを調べる」表を使ってきましたが、逆に「確率Pの値からKPを調べる」表もあります。これは(I)の表の逆引きにあたるものです。
正規分布表(II)PからKPを求める表(簡易版)
| P | .001 | .005 | .01 | .025 | .05 | .1 | .2 | .3 | .4 |
|---|---|---|---|---|---|---|---|---|---|
| KP | 3.090 | 2.576 | 2.326 | 1.960 | 1.645 | 1.282 | .842 | .524 | .253 |
正規分布表(III)PからKPを求める表(詳細版)
| P | *=0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0* | ∞ | 3.090 | 2.878 | 2.748 | 2.652 | 2.576 | 2.512 | 2.457 | 2.409 | 2.366 |
| 0.0* | ∞ | 2.326 | 2.054 | 1.881 | 1.751 | 1.645 | 1.555 | 1.476 | 1.405 | 1.341 |
| 0.1* | 1.282 | 1.227 | 1.175 | 1.126 | 1.080 | 1.036 | .994 | .954 | .915 | .878 |
| 0.2* | .842 | .806 | .772 | .739 | .706 | .674 | .643 | .613 | .583 | .553 |
| 0.3* | .524 | .496 | .468 | .440 | .412 | .385 | .358 | .332 | .305 | .279 |
| 0.4* | .253 | .228 | .202 | .176 | .151 | .126 | .100 | .075 | .050 | .025 |
使い方はシンプルです。たとえば、「確率P = 0.10(10%)のとき、KPはいくつか?」を調べるには、簡易版の表で「.1」の列を見ると、KP = 1.282と読み取れます。詳細版の表では、「0.1*」の行の「*=0」の列で同じ値が確認できます。
例題で実践|正規分布の確率を求めてみよう
ここまで学んだ内容を、例題で実践してみましょう。上の正規分布表(I)を参照しながら、一緒に解いていきます。
例題:部品の重さが正規分布に従うとき
ある工場で生産している部品の重さxが、正規分布N(150, 5²)に従っています。つまり、平均μ = 150g、標準偏差σ = 5gです。次の確率を求めてみましょう。
- (1) xが158g以上になる確率
- (2) xが143g以上156g以下になる確率
解き方のステップ
(1) xが158g以上になる確率
確率を求めるときは、まず図を描くことが大切です。平均μ = 150gを中心に釣鐘型の山を描き、求めたい値158gを横軸の右側にマークしましょう。「158g以上」の確率は、158gから右側の裾の面積にあたります。158gは平均150gより右側にあるので、正規分布表の確率をそのまま使えるパターン①に該当します。
ステップ1:標準化を行います。
Z = (x − μ) / σ = (158 − 150) / 5 = 1.60
ステップ2:正規分布表(I)からPを読み取ります。
|Z| = KP = 1.60です。表(I)の「1.6*」の行と「*=0」の列が交わるところを見ると、0.0548と読み取れます。
したがって、xが158g以上になる確率は5.48%です。1000個の部品を作ったら、約55個が158g以上になる計算です。
(2) xが143g以上156g以下になる確率
図を描いてみましょう。平均150gの山の中で、143gから156gまでの範囲に色を塗ります。今回求めたいのは真ん中の部分の面積なので、パターン③に該当します。「全体(1)から左右の裾の面積をそれぞれ引く」ことで求めます。
まず、143g以下になる確率を求めます。
Z = (143 − 150) / 5 = −1.40
|Z| = KP = 1.40です。表(I)の「1.4*」の行と「*=0」の列が交わるところを見ると、P = 0.0808と読み取れます。
次に、156g以上になる確率を求めます。
Z = (156 − 150) / 5 = 1.20
|Z| = KP = 1.20です。表(I)の「1.2*」の行と「*=0」の列が交わるところを見ると、P = 0.1151と読み取れます。
最後に、全体から両端を引きます。
1 − 0.0808 − 0.1151 = 0.8041
したがって、xが143g以上156g以下になる確率は80.41%です。つまり、この工場で作られる部品の約8割は、143g〜156gの範囲に収まるということです。
二項分布とは?|計数値の分布を理解しよう
正規分布が計量値(重さや長さなど)の分布を表すのに対して、二項分布は計数値(個数や人数など)の分布を表します。QC検定3級では、二項分布の出題頻度は低いですが、基本的な考え方は理解しておきましょう。
二項分布の考え方:成功か失敗かの2パターン
二項分布は、「結果が2通りしかない試行を繰り返したとき、成功が何回起こるか」を表す確率分布です。
「結果が2通り」とは、たとえば次のようなケースです。
- 製品を検査して「合格」か「不合格」か
- コインを投げて「表」か「裏」か
- 部品を確認して「良品」か「不良品」か
このように、毎回の結果が必ず2つのどちらかになる実験や検査を「試行」といいます。この試行を何回も繰り返したときに、「成功(たとえば不良品)が何個出るか」が従う分布が二項分布です。
たとえば、製造ラインからn個の製品を抜き出し、不適合品がx個含まれる確率をPとすると、「不適合品の個数xは二項分布B(n, P)に従う」といいます。
二項分布のパラメータ:試行回数nと確率P
二項分布の形を決めるパラメータは、試行の回数nと成功の確率Pの2つです。二項分布はB(n, P)と表します。
正規分布がN(μ, σ²)、二項分布がB(n, P)——この表記の違いは試験で問われることがあるので、セットで覚えておきましょう。
なお、二項分布B(n, P)の期待値はnP、分散はnP(1−P)、標準偏差は√{nP(1−P)}で求めることができます。試験ではあまり問われませんが、簡単な式なので頭の片隅に入れておくとよいでしょう。
xがとる値とパターン
具体例で考えてみましょう。製品を5個取り出して検査するとします(n = 5)。
もしP = 1(不適合品の確率が100%)なら、5個全てが不適合品です。取りうる値はx = 5の1通りだけです。逆にP = 0(不適合品の確率が0%)なら、x = 0の1通りだけです。
しかし現実には、0 < P < 1(0%より大きく100%より小さい)のケースがほとんどです。この場合、不適合品の個数xは0個、1個、2個、3個、4個、5個のどれにもなりえます。つまり、6通りの値をとります。
たとえ不適合品の確率がわずか5%(P = 0.05)だとしても、確率が0でない限り、運悪く5個全てが不適合品になる可能性はゼロではないのです。
xの発生する確率の計算
もう少しシンプルな例で計算してみましょう。製品を4個取り出し(n = 4)、不適合品の確率がP = 0.2(20%)の場合を考えます。
1つの製品が不適合品である確率は0.2、良品である確率は1 − 0.2 = 0.8です。
確率を計算するときに大切なのは、「どの製品が不適合品になるか」の組み合わせを考えることです。
不適合品x = 0のとき(4個とも良品):
0.8 × 0.8 × 0.8 × 0.8 = 0.4096
組み合わせは1通りなので、確率は0.4096です。
不適合品x = 1のとき(1個が不適合品):
「1つ目が不適合品で残り3つが良品」「2つ目が不適合品で残りが良品」「3つ目が」「4つ目が」の4通りの組み合わせがあります。
1通りあたりの確率:0.2 × 0.8 × 0.8 × 0.8 = 0.1024
0.1024 × 4 = 0.4096
不適合品x = 2のとき(2個が不適合品):
4個の中からどの2個が不適合品になるかの組み合わせは6通りあります。
1通りあたりの確率:0.2 × 0.2 × 0.8 × 0.8 = 0.0256
0.0256 × 6 = 0.1536
不適合品x = 3のとき(3個が不適合品):
組み合わせは4通りあります。
1通りあたりの確率:0.2 × 0.2 × 0.2 × 0.8 = 0.0064
0.0064 × 4 = 0.0256
不適合品x = 4のとき(4個とも不適合品):
0.2 × 0.2 × 0.2 × 0.2 = 0.0016
組み合わせは1通りなので、確率は0.0016です。
全てを合計すると、0.4096 + 0.4096 + 0.1536 + 0.0256 + 0.0016 = 1.0000となり、確率の合計がぴったり1(100%)になることが確認できます。全ての可能性を漏れなく数え上げた証拠です。
正規分布と二項分布の違い|試験で混同しないためのポイント
正規分布と二項分布は、どちらも確率分布ですが、扱うデータの種類が根本的に異なります。試験本番で迷わないように、違いをすっきり整理しておきましょう。
正規分布は計量値(長さ、重さ、温度など「測る」データ)の分布です。パラメータは平均μと分散σ²で、N(μ, σ²)と表します。形は左右対称の釣鐘型で、QC検定3級での出題頻度は非常に高いです。
二項分布は計数値(不適合品数、人数など「数える」データ)の分布です。パラメータは試行回数nと確率Pで、B(n, P)と表します。QC検定3級での出題頻度は低く、基本的な考え方が問われる程度です。
見分けるコツはシンプルです。問題文のデータが「測るもの」(重さ152.3g、長さ25.1mmなど小数点がつくデータ)なら正規分布、「数えるもの」(不適合品3個、合格者12人など整数のデータ)なら二項分布と判断しましょう。
まとめ|試験で押さえるべき重要ポイント
最後に、この記事で解説した内容の中から、試験当日に必ず使う重要ポイントをまとめます。
正規分布について:正規分布は「測る」データ(計量値)の分布です。パラメータは平均μと分散σ²で、N(μ, σ²)と表します。形は左右対称の釣鐘型。平均μが0、分散σ²が1の正規分布N(0, 1²)が標準正規分布で、正規分布表のもとになっています。
標準化について:どんな正規分布でも、標準化の式「Z = (x − μ) / σ」を使えば標準正規分布に変換でき、正規分布表で確率が読み取れます。この式は試験で最も使う公式の1つです。
確率の求め方について:正規分布の確率を求める問題は3つのパターンに分類できます。「図を描いて、求めたい面積がどこかを確認してから計算する」——この手順を守れば、どのパターンでも確実に解けます。
二項分布について:二項分布は「数える」データ(計数値)の分布です。パラメータは試行回数nと確率Pで、B(n, P)と表します。3級では出題頻度が低いですが、正規分布との違いを問う問題に備えて、基本を押さえておきましょう。
正規分布の問題は、QC検定3級の合否を左右する重要な得点源です。この記事で紹介した手順を繰り返し練習して、試験本番で自信を持って解答できるようにしましょう。




